In principal components analysis, "Variables measured on different scales or on a common scale with widely differing ranges are often standardized." Relative importance of variables in multiple regression: Standardized regression coefficients "For some multivariate techniques such as multidimensional scaling and cluster analysis, the concept of distance between the units in the data is often of considerable interest and importance… When the variables in a multivariate data set are on different scales, it makes more sense to calculate the distances after some form of standardization." Principal components analysis Percentage of observations below a z-score Ĭontinuing the example of ACT and SAT scores, if it can be further assumed that both ACT and SAT scores are normally distributed (which is approximately correct), then the z-scores may be used to calculate the percentage of test-takers who received lower scores than students A and B.Ĭluster analysis and multidimensional scaling X is converted into a standard score by z = x − μ σ īecause student A has a higher z-score than student B, student A performed better compared to other test-takers than did student B. If the population mean and population standard deviation are known, a raw score
3 Standardizing in mathematical statistics. 2.8 Relative importance of variables in multiple regression: Standardized regression coefficients. 
2.6 Cluster analysis and multidimensional scaling. 2.5 Percentage of observations below a z-score. 2.4 Comparison of scores measured on different scales: ACT and SAT. Ĭomputing a z-score requires knowing the mean and standard deviation of the complete population to which a data point belongs if one only has a sample of observations from the population, then the analogous computation with sample mean and sample standard deviation yields the t-statistic. Other terms include z-values, normal scores, standardized variables and pull in high energy physics. Standard scores are most commonly called z-scores the two terms may be used interchangeably, as they are in this article. This process of converting a raw score into a standard score is called standardizing or normalizing (however, "normalizing" can refer to many types of ratios see normalization for more). It is calculated by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores. In statistics, the standard score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Includes: Standard deviations, cumulative percentages, percentile equivalents, Z-scores, T-scores Multiply the feet by 12.Compares the various grading methods in a normal distribution. To convert an engineering drawing scale to a scale factor: Invert the fraction and multiply by 12. To convert an architectural drawing scale to a scale factor: Said a different way by Autodesk, "You can change the view scale of the viewport by using the XP option of the ZOOM command when model space is accessed from within a layout viewport." Calculating Scale Factor For instance, you would be in paper space on a sheet, then you would enter model space within the viewport, then you would type Z or Zoom and enter 96xp to scale the drawing to 1/8" = 1'-0" in paper space. The suffix is AutoCAD nomenclature for changing the scale within a viewport. You will notice that the Viewport Scale in the charts below indicate a scale with the suffix XP. However, since these drawings get placed on sheets of paper that are much smaller, a scale factor is required so that the final drawing has a usable conversion factor. 
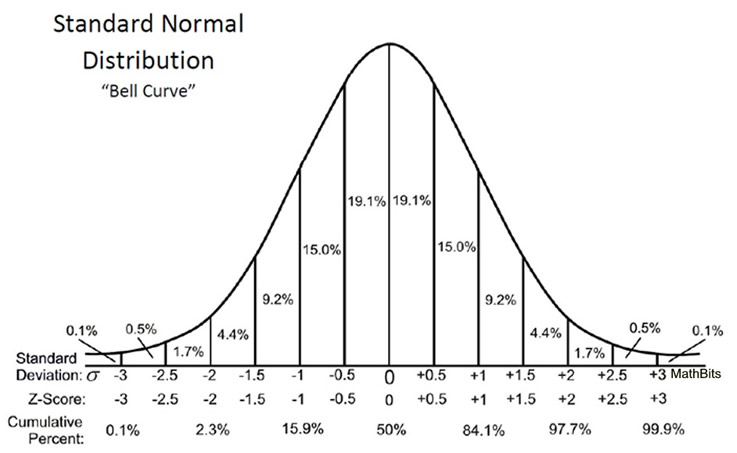
For instance, when drawing a door in CAD, the door would be 3 feet wide and 7 feet tall.
For simplicity and clarity, CAD users draw buildings at full scale.
0 kommentar(er)
